Let's talk about GEB

写在前面：在完成这次读书笔记的过程中，由于准备时间的不充分和GEB此书内容之庞杂，我尝试了一种AI协作的策展式写作方法，也就是我负责策划整体的叙事逻辑，在必要的位置向AI提出需求，AI生成片段化的内容。在这种方式的辅助下，我可以专注在如何搭建更好的内容框架和叙述逻辑，如何在不同板块之间寻找联系，而不必费心于每个内容板块内的文字搭建。

开始之前，我们先聊聊一个程序

元胞自动机：生命来自哪里

元胞自动机是一种程序化的游戏，它有着极其简单的规则——却最终可以得到复杂的生命形态。运动、自动的图灵机（兰顿蚂蚁），都可以从元胞自动机中找到。甚至还有自指。

• 每个细胞有两种状态 - 存活或死亡，每个细胞与以自身为中心的周围八格细胞产生互动
• 当前细胞为存活状态时，当周围的存活细胞低于2个时（不包含2个），该细胞变成死亡状态。（模拟生命数量稀少）
• 当前细胞为存活状态时，当周围有2个或3个存活细胞时，该细胞保持原样。
• 当前细胞为存活状态时，当周围有超过3个存活细胞时，该细胞变成死亡状态。（模拟生命数量过多）
• 当前细胞为死亡状态时，当周围有3个存活细胞时，该细胞变成存活状态。（模拟繁殖）

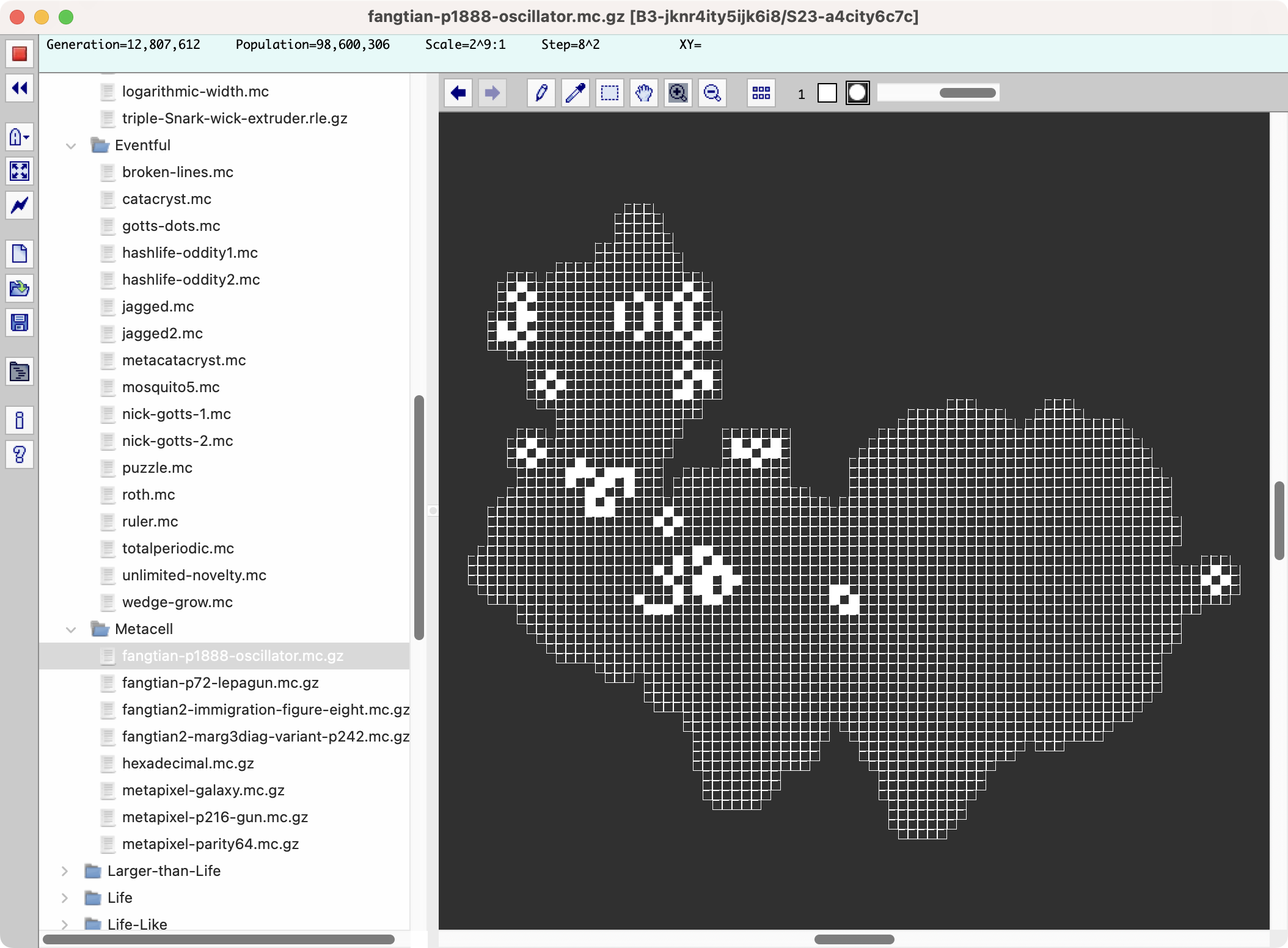
Metacell-细胞组成的细胞，细胞的自指

from Golly

Q：能不能把元胞自动机视为生命？生命的特征是什么？

命运的2个方面：

1. Conway game of life：同一规则下，起点对结果的巨大影响

2. 兰顿蚂蚁：不同起点下，最终一样的结局（1w步以后都会走上高速公路）

说到生命，我们都认为生命的遗传和DNA密切相关，那么应该如何理解DNA？

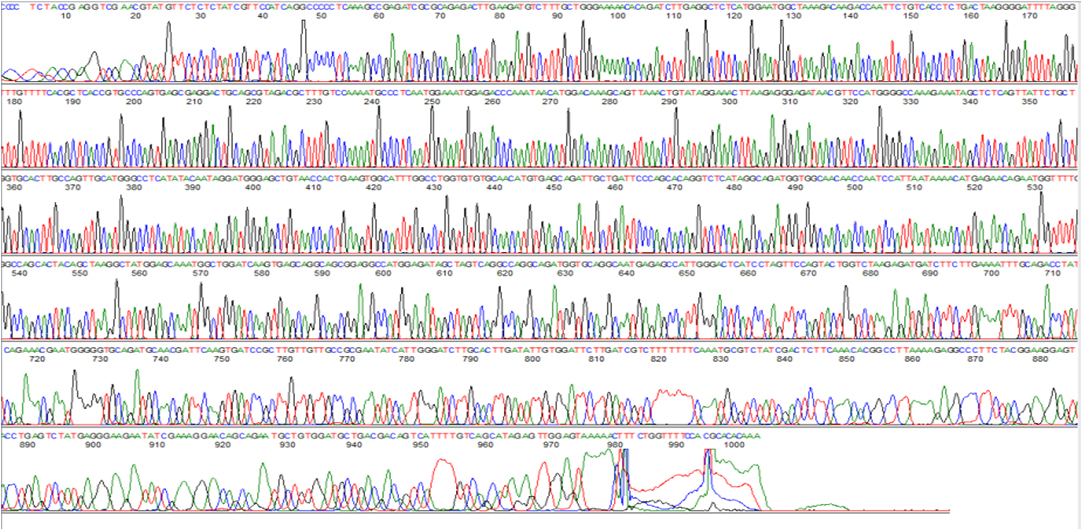
一段染色体序列，四种颜色代表四种碱基

from Google

我们一般一厢情愿地认为 不同碱基段的排列代表了一个基因，而这个基因体现在生物的某个性征上。比如皮肤颜色、遗传病。

但是我们很难把一个生物和它的DNA完全对应起来。

DNA=触发开关+规则。开关引发了按照规则进行的动作，但是动作逐步产生的结果不可预测。严格的物理意义上的碱基序列可以解释一部分遗传现象，但是却无法解释人类意识、个体差异的鸿沟。

作者其人

侯世达本人

侯世达（Douglas Hofstadter） 认知和计算机科学家，研究意识、怪圈、AI之间的关联，为了探索自我和意识的本质，他于1979年写作了 Gödel, Escher, Bach: An Eternal Golden Braid 。获得了普利策奖的大众非虚构类。

• 全书的核心问题：“人类心智如何从机械的符号操作中涌现？”（即“意识是否可还原为形式系统？”）

• 自我（self）是如何从没有自我（non-self）的事物中产生的

• 这些无意识的原子、分子、蛋白质是怎么一步步形成了有意识的实体的

关键概念: 形式系统

WU谜题：形式系统、系统内外、判定过程

从一个预设的WJU形式系统开始，以WJ字符串为系统的起始，基于以下4条推导规则，是否能得出WU。

• 规则1：WJ后可以跟上U

• 规则2：Wx可以替换为Wxx，其中x为任意字符串

• 规则3：每处JJJ可以替换为U

• 规则4：每处UU可以被直接去掉

Q：你发现了什么？你是怎么做的？

大多数人，开始时，想通过在系统内部工作解决WU谜题；逐渐地，你开始着急了，这种焦急心情增长到一定程度时就不再作任何考虑地退出了这个系统，然后盘算一下产生了一些什么，想想为什么没有取得成功——即产生出WU。也许你发现了没能产生出WU的原因所在，这是对于系统进行思索。也许你在中途什么时候产生了WJU，这是在系统之内进行工作。 This is meta thinking：跳出体系

pq系统

pq系统有无数个公理。但这些公理可以用一个共同的模式生成，即x-pxq-，其中x只由横杠-组成，在公理以外，有着一条简洁的推导规则，得到所有的定理：

• 若xpyqz是一条定理，那么x-pyqz-也是一条定理

-p-q– 是不是可以被解读为1+1=2?

p可以解释为plus，q解释为equal。那么这个系统就是加法。

形式系统本无意义，需要解读者赋予意义，这和语言中的意义就不一样。语言中的意义是主动的

现在再想想1+1=2。有没有可能1+1=1？1+1=0?

WJU、pq 所构筑的世界就是形式系统。形式系统是由符号、规则（语法）和公理（初始命题）构成的封闭逻辑世界，例如欧几里得几何、数理逻辑或国际象棋。它像一台精密的机械钟表，所有结论必须通过既定规则从公理推导而来，排除一切主观性与模糊性。

ok，现在我们知道了形式系统是什么，这样，对意识/意义的研究，就不必在复杂的现实世界中推导，而是可以基于简化的形式系统中

当然，形式系统也和哥德尔不完备定理的证明密切相关

自指悖论

形式系统是一个确定的理想世界，符号 + 规则 + 公理 → 封闭的推导世界，可预测，机械性。而自指悖论则是在这个理想世界里放置一面「镜子」

• “这句话是假的” → 经典说谎者悖论

• 小镇理发师悖论

• 罗素悖论：普通集合和自吞集合，例如包括所有集合的集合。

自指让系统被迫“跳出自身”审视自己，暴露其局限性。

层次跳跃

当一个系统讨论自身时，必须进入更高层级（元层）。系统无法在自身内部完全描述元层。

• 小说中的角色读到一本描写自己故事的书。

• 在元数学的层次，才能讨论数学本身的问题

寻找一个核心问题：

形式系统如同一个透明的玻璃迷宫，人们可以清晰观察符号如何按规则运动。如果意识是符号操作的结果，那为什么迷宫会诞生“观察迷宫自身”的视角？

⬇️

如果大脑是一个由神经元（符号）和生物规则（语法）构成的复杂形式系统，为何会产生“自我意识”这种看似超越规则的现象？

答案：怪圈

定义：系统通过不同层次的递归自指，形成一种既封闭又开放的动态的自我观察结构（如大脑神经元活动产生“我”这一观察者）。通过自指和递归在不同层次间跳跃，最终模糊系统边界的动态结构。这种结构既逻辑严密又自我矛盾，既封闭又开放，既是机械的又涌现出超越机械性的意义。

• 自指（Self-reference）：系统的一部分指向自身或系统的其他部分。

• 层次跳跃（Level-jumping）：在不同逻辑层级间循环，例如从“对象层”跳到“元层”（如关于自身的描述）。

• 闭环与开环的矛盾：看似闭合的循环，实则无法真正闭合，导致逻辑上的悖论或意义的涌现。

想象一面镜子对着另一面镜子，镜中影像无限递归，但物理上镜子本身是有限的——这种“有限中的无限感”就是怪圈。或如一条蛇咬住自己的尾巴（衔尾蛇），形成一个循环，但蛇头与蛇尾在逻辑上无法真正闭合。

形式系统的角色：形式系统是怪圈的“机械基础”，而怪圈是形式系统的“自我超越”。就像埃舍尔的《画手》，两只手互相绘制对方，既是机械过程的产物，又是对机械过程的否定。

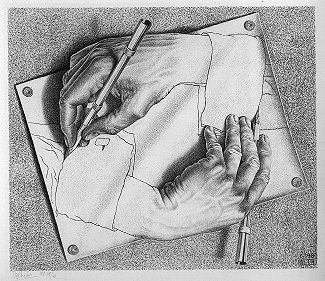
埃舍尔的《画手》（Drawing Hands）

巴赫的《螃蟹卡农》：音符正向与逆向同时演奏，规则严格却涌现出超越规则的美感。

怪圈让我们发现有限中的无限，哥德尔的数学证明、埃舍尔的视觉奇观、巴赫的卡农复调本质上都是形式规则下的递归创造

Maurits Cornelis Escher (1898-1972) ‘Print gallery'

观众凝视画中的城市，而城市中的画廊又包含了观众自身——这种视觉递归正是形式系统自指的隐喻，从而形成一种无限嵌套的递归结构。

数学系统试图描述自身时，会形成不可避免的自指性，最终导致系统边界的模糊化。

侯世达认为人的自我意识也是一种“递归嵌套结构”，即意识是大脑不断自我反映的产物。

首先有一个形式系统，比如神经元和电流组成的大脑。之后大脑通过自指，形成递归循环，产生了主观意识。

意识无法被还原为纯粹的物理活动，因为它具备不同层次的跃迁特点，动态传递。所谓意识中的「自由意志」，或许就源自怪圈中不可预测的层次跳跃

三位大师

埃舍尔：绘画

相对论

乐高搭建的相对论

相对论——

这与GEB中的意义的自创（Self-Referential Meaning Creation）一致，即在不同的参考系下，系统的解释是多义的，没有单一固定的真相。

也符合侯世达的观点：意识并非一个固定不变的结构，而是取决于观察角度的动态系统。

Metamorphosis II

https://www.digitalcommonwealth.org/search/commonwealth:ww72cb78j

从棋盘格变成动物、建筑物，最终回到起点，形成一个循环。

与GEB中的巴赫赋格高度一致：一个音乐主题在不断变化和转换中，最终回到原点。

也类似于数理逻辑中的“从公理到定理再回到公理”的数学发展循环。

数学家时期的埃舍尔绘画

Mandelbrot set：

$$ fc(z)=z^2+c $$

其中c是一个复数参数。

从z=0 开始对fc(z)进行迭代：

$$z_{n+1}=z_{n}^{2}+c,n=0,1,2,…$$

$$z_{0}=0$$

$$z_{1}=z_{0}^{2}+c=c$$ $$z_{2}=z_{1}^{2}+c=c^{2}+c$$ 每次迭代的值依序如以下序列所示： $$(0,f_{c}(0),f_{c}(f_{c}(0)),f_{c}(f_{c}(f_{c}(0))),\ldots )$$

不同的参数c可能使序列的绝对值逐渐发散到无限大，也可能收敛在有限的区域内。

曼德博集合M就是使序列不延伸至无限大的所有复数 c的集合。

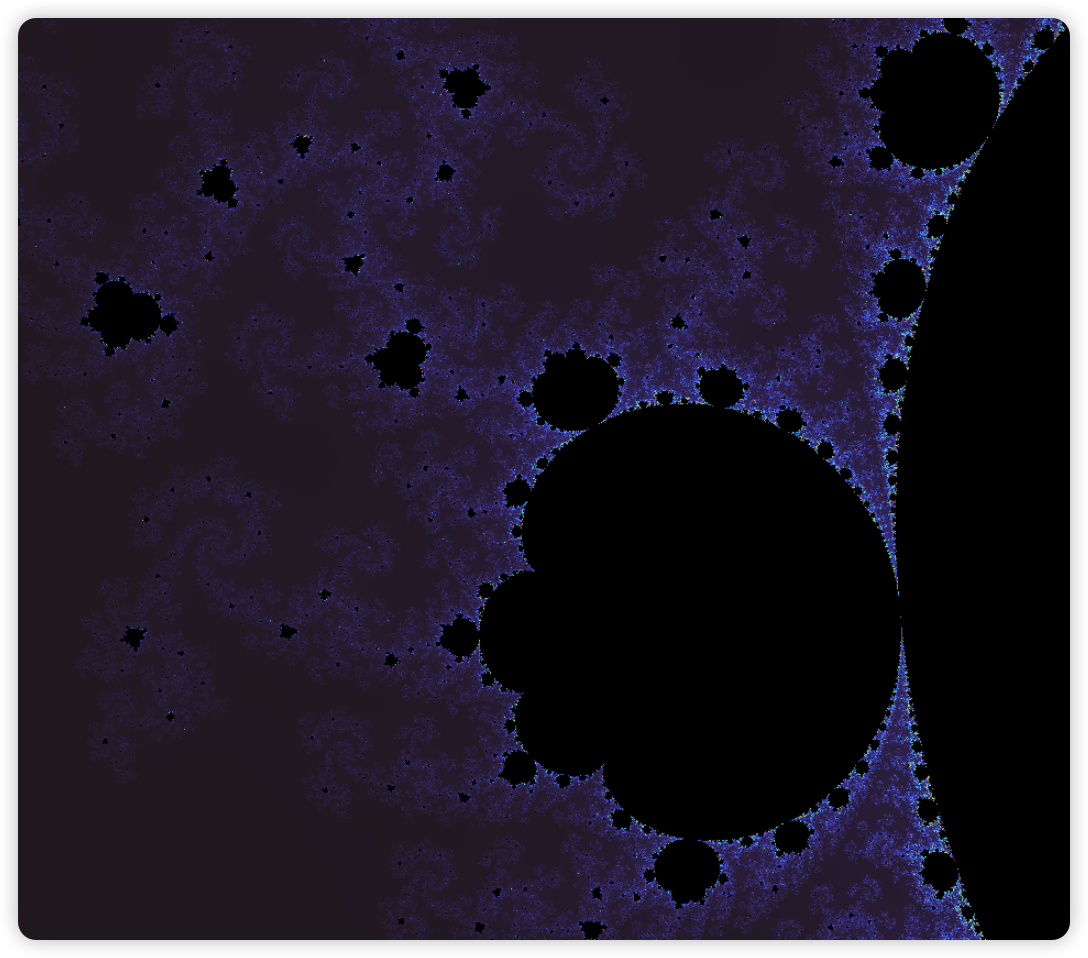
曼德博集合

https://mandelbrot.site/

巴赫：音乐

《音乐的奉献》（Musical Offering, BWV 1079）

https://www.youtube.com/watch?v=W5Rk6Fqbo3Y&ab_channel=anvesir

这是巴赫根据腓特烈大帝给出的一个主题即兴创作的作品，包含赋格、卡农和奏鸣曲等多种形式。

• 其中的“逆行卡农”（Crab Canon）是一种高度对称的结构，正着弹和倒着弹都能形成相同的音乐逻辑。

• 这首曲子表现了递归性（Recursive Structures）和自指性（Self-Reference）

• 侯世达在GEB的文本结构中直接模仿了此曲，设计了一段可以前读后读都能成立的对话。

《哥德堡变奏曲》（Goldberg Variations, BWV 988）

• 主题由 30 个变奏组成，其中结构严谨，每 3 个变奏形成一个小组，最后回到最初的主题，形成闭环结构。

• 其中“倒影卡农”（Mirror Canon）、“二度卡农、三度卡农……九度卡农”展现了不同层次上的递归关系。

《哥德堡变奏曲》的结构呼应了GEB的叙述方式：GEB 中的每一章都是一组自指性的对话，主题不断变化但仍保留整体逻辑。

变奏的方式类似于哥德尔定理中从公理推导新定理的过程：每个变奏都是在规则的限制下产生的新层次，而这些层次最终回归到原点。

《赋格的艺术》（The Art of Fugue, BWV 1080）

• 这是巴赫晚年的作品，探索了赋格的极限。赋格是一种高度结构化的作曲形式，核心特征包括递归、模仿和层级嵌套。

• 其中未完成赋格（Contrapunctus XIV），其主题正是巴赫自己名字B-A-C-H（在德国音名中，B=降B，A=A，C=C，H=B），形成了音乐中的“自指”。

赋格的核心是递归（Recursion）：在不同的声部中，主题反复出现，但每次都以不同方式进行变形和组合。

巴赫在音乐中加入了自己名字的主题，形成自指（Self-Reference），这正是GEB中哥德尔公式“这个命题无法被证明”的数学类比。

《平均律钢琴曲集》（The Well-Tempered Clavier, BWV 846-893）

• 这是一套包含 24 个大小调前奏曲与赋格的钢琴曲，探索了十二平均律的可能性。

• 每一首赋格都有不同的模仿技巧，如逆行、倒影、增减值等。

这与哥德尔不完备定理的逻辑类似：在特定规则下（赋格的作曲法），可以无限生成新命题（新变奏），但整体结构仍然保持一致。

侯世达认为“赋格”象征了人类的思维过程：多个思想（旋律）同时存在，它们互相影响，形成意识的怪圈。

哥德尔不完备定理

哥德尔通过将符号映射为数字（哥德尔数），让数学系统“自我描述”，从而在系统内部制造悖论。

哥德尔通过天才的证明过程，意在说明一件事情：

任何一个能作为数学基础的公理集都不可避免地是不完备的：总有一些关于数的事实不能被这些公理证明。没有任何一个候选的公理集能够证明其自身的一致性。

STEP1 哥德尔数映射

用12个基本符号作为词汇来表达一系列基本公理。例如，用符号 ∃ 表示存在，用符号 + 表示加法。重要的是，符号 s 表示“后继”，给出了表示特定数字的方法。例如， ss0 指的是 2 。这12个符号被分配到了从1至12的哥德尔数。

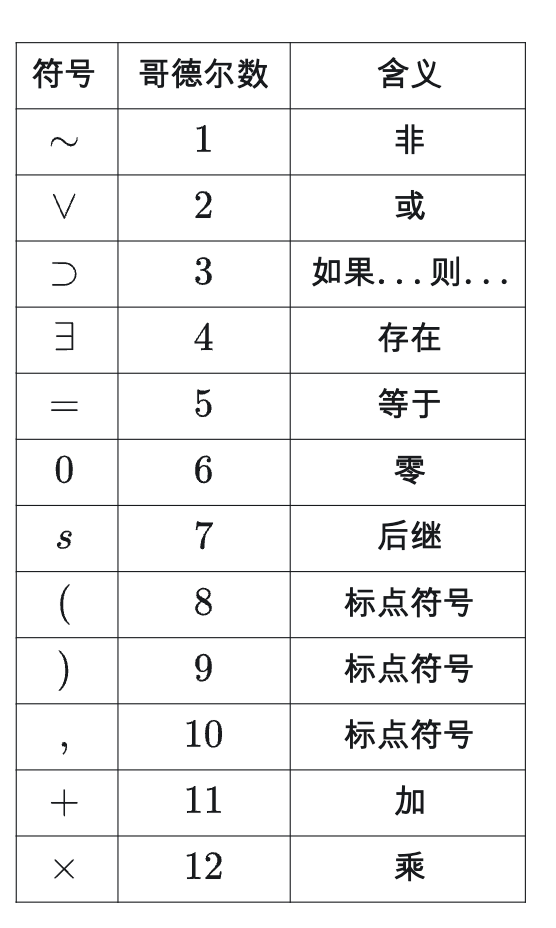
12个符号的哥德尔数映射

用字母表示变量，从 x,y,z 开始，映射到大于12的素数（即 13,17,19,… ）。

考虑 0=0 。这个公式的三个符号对应的哥德尔数是 6,5,6 。哥德尔需要将这三个数字的序列改为一个唯一的数字，也就是其他符号序列不会生成的数字。 为此，他采用前三个质数（2,3,5）将每个符号的哥德尔数作为这个序列相同位置的指数，并将它们相乘。因此 0=0 变为 2^6×3^5×5^6，即 243000000。

STEP2: G 自身

$$(∃x)(x=sy)$$ 它读作“存在一个变量 x 使得它是 y 的后继”，或者简言之，“ y有一个后继”。像所有公式一样，它有哥德尔数，即某个大整数，我们就叫它 m。

把y替换成m

$$(∃x)(x=sm)$$

新的公式的哥德尔数是：$$sub(m,m,17)$$

sub(a,b,c)是一个新的函数，第一个参数a是一个公式的哥德尔数，c指的是符号的哥德尔数。然后在a（反向解码为公式）中对应c的符号位置替换成b。那么新的公式的哥德尔数就是sub(a,b,c)

元数学语句“无法证明哥德尔数为 sub(y,y,17)的公式” 这个语句的哥德尔数是n

最后一轮替换：将数字 n 替换先前公式中 y 的位置来创建一个新公式。他的新公式声称：“无法证明哥德尔数为 sub(n,n,17) 的公式”。我们将此新公式称为 G 。

G的哥德尔数是什么？肯定是sub(n,n,17)

哥德尔定理是作为他一九三一年的一篇论文中的命题Ⅵ而出现的，这篇论文的题目是：“论《数学原理》及有关系统中形式上不可判定的命题Ⅰ”。该命题是这样叙述的：

对公式的每个ω一致的递归类κ，对应着一个递归的类记号γ，使得ν Gen γ或Neg(ν Gen γ)都不属于Flg(κ)（其中ν是γ的自由变量）。

原文是德文，其实意思就是

数论的所有一致的公理化形式系统都包含有不可判定的命题。

• 任何足够强的形式系统都存在无法自证的真命题

小结

我对这种theory of everything的书非常感兴趣，此类书籍数量并不多见，对作者的知识面要求很高。但是读起来最有一种和作者对话的感觉，ta因为自知内容的跨度，因此极为迫切地想要让你紧跟他的思路。

本书是以一种不同寻常的方式构成的：在对话和章节之间有一种对位。这样构造的目的是为了能够让一个新的概念出现两次：几乎每一个新概念都是首先以隐喻的形式出现在对话中，给出一组具体可见的意象，然后，在阅读接下来的那一章的时候，它们可以作为一种直观背景来衬托对这同一个概念的更为严肃和更为抽象的表述。在许多对话中，我在表面上谈论着一个想法，但是实际上是以稍稍隐蔽的方式在谈论着另一个想法。

另外，这本书的翻译也非常有趣，在作者的前言中（这是少有的非常值得一读的前言），他不断谈论80年代本书翻译遇到的佚事——对文本内容本地化的思考，和国内译者的协作——也让这本书的中文翻译本身和书的内容相得益彰。不过，文本本身有时还是颇为晦涩，或者没有触及作者要说的真正内核（他可能觉得过于抽象），因此这篇文章本身其实也来自很多其他人对GEB的解读延展，可能和原书内容有些许偏差，还请谨慎采纳。